SAC算法

本文最后更新于 2024年9月11日下午

前言

不过，SAC本身介绍的能量模型和最大熵模型内容已经能够形成一条完备的逻辑链了。从基本模型开始，看看SAC这一条路径到底干了些什么吧~

1、最大熵模型

1.1 为什么要用最大熵模型

传统的强化学习的目的是找出一个策略来最大化奖励，即目标函数：

\[ π^*= \arg \max _{\pi}\mathbb {E}_{(st,at)∼π}[\Sigma_tR(s_t,a_t)] \] 而最大熵强化学习是在最大化奖励的同时最大化熵： \[ π^*= \arg \max _{\pi}\mathbb {E}_{(st,at)∼π}[\Sigma_tR(s_t,a_t)+\alpha H(\pi(·|s_t))] \]

信息熵的公式为：$H(X)=−\sum_{i=1}^np(x_i)log⁡p(x_i)$ 用来表示

这样子做有几个好处：

加强探索。利用熵让每一步的决策增加随机性，相当于强化了RL中的探索。这一方面能够加速之后的学习，另一方面可以防止策略过早地收敛到局部最优解。
变确定性策略为随机策略。学过博弈论的小伙伴可能知道，在进行博弈时一个人的最优策略往往是混合策略，即随机策略往往是最优策略。增加熵可以增强策略的随机性，从而有助于收敛到最优策略。
作为复杂任务的初始化。最大熵策略不仅学到一个策略，还能够捕获到所有的行为模式，这类似于CV、NLP中预训练的想法，先训练一个捕获到很多模式的模型，再微调参数应用到自己的模型，这大大加快了训练的速度。
加强鲁棒性。仅仅最大化奖励的话，策略倾向于只找到一条路径，如果这条路径短了，那策略的表现就会迅速下降；而最大熵策略可以找到所有的行为模式，就算一条路径断了，还可以从另一条路径达到同样的结果。

1.2 SAC的最大熵模型的不同之处

其实，在SAC之前，很多强化学习算法都用到了熵作为正则化参数来增强策略的探索。

A3C：

∇θ′log⁡π(at∣st;θ′)(Rt−V(st;θv))+β∇θ′H(π(st;θ′))

PPO：

LtCLIP+VF+S(θ)=E^t[LtCLIP(θ)−c1LtVF(θ)+c2H[πθ](st)]

PGQL：

Δθ∝Es,aQπ(s,a)∇θlog⁡π(s,a)+αE∇θHπ(s)s

class Student: def init(self): self._age = 20 @property def age(self): return self._agestudent = Student()# 设置属性student.age = 18'''报错：property 'age' of 'Student' object has no setter'''# 获取属性，print('学生年龄为：' + str(student.age))"""输出学生年龄为：20"""#只有通过内部属性才能更改值，更加安全student._age = 18print('学生年龄为：' + str(student.age))"""输出学生年龄为：18"""python

这个地方也有人认为SAC的熵经过策略梯度定理推导之后等价于A3C的熵，不过无论如何，SAC的文章真正从理论上分析了VQπ中熵的存在性和可行性

1.3 从贝尔曼方程理解最大熵模型的值函数

借用了下这个画的图

1）首先看看普通强化学习的目标函数： \[ \pi^{*}=\arg \max _{\pi} \mathbb{E}_{\left(s_{t}, a_{t}\right) \sim \rho_{\pi}}\left[\sum_{t} R\left(s_{t}, a_{t}\right)\right] \]

其贝尔曼方程为：

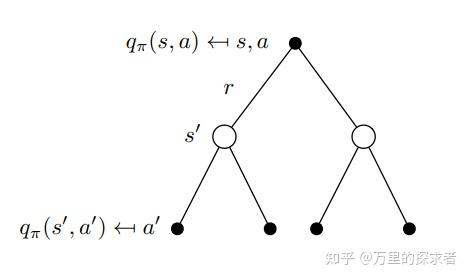
回溯图

从回溯图的角度，容易看到树的根结点$q_{\pi}(s, a)$ 实际上就是$r$与 $q_{}(s^{}, a^{}) $的期望的和。

2）再看看最大熵强化学习的目标函数： \[ \pi^{*}=\arg \max _{\pi} \mathbb{E}_{\left(s_{t}, a_{t}\right) \sim p_{\pi}}[\sum_{t} \underbrace{R\left(s_{t}, a_{t}\right)}_{\text {reward }}+\alpha \underbrace{H\left(\pi\left(\cdot \mid s_{t}\right)\right)}_{\text {entropy }}] \]

这个 $\alpha$ 是温度系数，用来衡量熵项的重要程度，后面的推导中如果没有写这一项的话是因为默认值为1。

可以看到这个熵是加在状态上的，和动作无关。反映到回溯图中，就是：

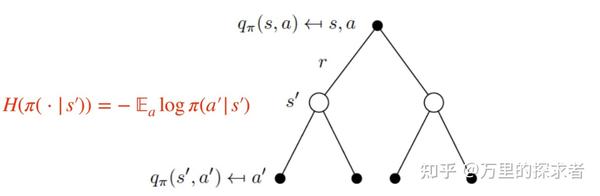
加了熵的回溯图

类比一下，可以把$H ((|s^)) $看作是状态价值函数，把$(a_{t+1}|s_{t+1} )$看作动作价值函数，那么：$$ H ((|s_{t+1}))=-{a{t+1} A}p(a_{t+1}|s_{t+1})(a_{t+1}|s_{t+1} )=-{a{t+1} }(a_{t+1}|s_{t+1} ) $$ 即在一个状态下的熵=在这个状态下对于每一个动作的可能性进行求期望，再反映到回溯图中，就可以看到熵和q是可以写在一起的：

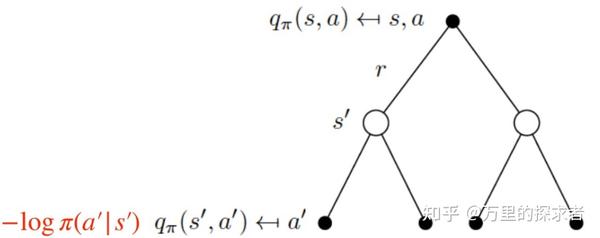
熵拆解后的回溯图

于是贝尔曼方程可以写为：

\[ Q\left(\mathbf{s}_{t}, \mathbf{a}_{t}\right) \leftarrow r\left(\mathbf{s}_{t}, \mathbf{a}_{t}\right)+\gamma \mathbb{E}_{\mathbf{s}_{t+1} \sim p, \mathbf{a}_{t+1} \sim \pi}\left[Q\left(\mathbf{s}_{t+1}, \mathbf{a}_{t+1}\right)-\log \pi\left(\mathbf{a}_{t+1} \mid \mathbf{s}_{t+1}\right)\right] \] 而我们知道在之前的强化学习中，贝尔曼方程中Q与V的关系是：

\[ Q\left(\mathbf{s}_{t}, \mathbf{a}_{t}\right) \triangleq r\left(\mathbf{s}_{t}, \mathbf{a}_{t}\right)+\gamma \mathbb{E}_{\mathbf{s}_{t+1} \sim p}\left[V\left(\mathbf{s}_{t+1}\right)\right] \] $p=p(s_{t+1}|s_t)$即从状态$s_{t}$转移到$s_{t+1}$的状态转移分布或概率函数，就是状态转移的概率。

因此，对比以上两式，就可以定义$V$函数：

\[ r\left(\mathbf{s}_{t}, \mathbf{a}_{t}\right)+\gamma \mathbb{E}_{\mathbf{s}_{t+1} \sim p, \mathbf{a}_{t+1} \sim \pi}\left[Q\left(\mathbf{s}_{t+1}, \mathbf{a}_{t+1}\right)-\log \pi\left(\mathbf{a}_{t+1} \mid \mathbf{s}_{t+1}\right)\right]=r\left(\mathbf{s}_{t}, \mathbf{a}_{t}\right)+\gamma \mathbb{E}_{\mathbf{s}_{t+1} \sim p}\left[V\left(\mathbf{s}_{t+1}\right)\right] \\ \gamma \mathbb{E}_{\mathbf{s}_{t+1} \sim p, \mathbf{a}_{t+1} \sim \pi}\left[Q\left(\mathbf{s}_{t+1}, \mathbf{a}_{t+1}\right)-\log \pi\left(\mathbf{a}_{t+1} \mid \mathbf{s}_{t+1}\right)\right]=\gamma \mathbb{E}_{\mathbf{s}_{t+1} \sim p}\left[V\left(\mathbf{s}_{t+1}\right)\right] \\ V\left(\mathbf{s}_{t}\right)=\mathbb{E}_{\mathbf{a}_{t} \sim \pi}\left[Q\left(\mathbf{s}_{t}, \mathbf{a}_{t}\right)-\log \pi\left(\mathbf{a}_{t} \mid \mathbf{s}_{t}\right)\right] \]

1.4 直接从公式理解值函数

1.3节从贝尔曼方程的角度理解了值函数之间的关系，不过说到底还是图像化的理解，从公式的角度出发其实可以直接定义出来$Q、V$，就是没1.3那么好理解而已。不过从严谨性的角度，公式化的定义是非常有必要的。

1）首先看看标准的$Q、V$函数，其被定义为条件化的累积奖励： \[ Q_{\pi}(s, a)=\underset{s_{t}, a_{t} \sim \pi}{\mathbb{E}}\left[\sum_{t=0}^{\infty} \gamma^{t} r\left(s_{t}, a_{t}\right) \mid s_{0}=s, a_{0}=a\right] \\ V_{\pi}(s)=\underset{s_{t}, a_{t} \sim \pi}{\mathbb{E}}\left[\sum_{t=0}^{\infty} \gamma^{t}\left(r\left(s_{t}, a_{t}\right)\right) \mid s_{0}=s\right] \]

2）类似的，可以定义出最大熵版本的Q和V： \[ \begin{aligned} Q_{s o f t}^{\pi}(s, a) =\underset{s_{t}, a_{t} \sim \rho_{\pi}}{\mathbb{E}}\left[\sum_{t=0}^{\infty} \gamma^{t} r\left(s_{t}, a_{t}\right)+\alpha \sum_{t=1}^{\infty} \gamma^{t} H\left(\pi\left(\cdot \mid s_{t}\right)\right) \mid s_{0}=s, a_{0}=a\right] \end{aligned} \]

\[ V_{s o f t}^{\pi}(s)=\underset{s_{t}, a_{t} \sim \rho_{\pi}}{\mathbb{E}}\left[\sum_{t=0}^{\infty} \gamma^{t}\left(r\left(s_{t}, a_{t}\right)+\alpha H\left(\pi\left(\cdot \mid s_{t}\right)\right)\right) \mid s_{0}=s\right] \]

从Q的定义出发，同样可以推出贝尔曼方程：

\[ \begin{aligned} Q_{s o f t}^{\pi}(s, a) &=\underset{\substack{s^{\prime} \sim p\left(s^{\prime} \mid s, a\right) \\ a^{\prime} \sim \pi}}{\mathbb{E}}\left[r(s, a)+\gamma\left(Q_{\text {soft }}^{\pi}\left(s^{\prime}, a^{\prime}\right)+\alpha H\left(\pi\left(\cdot \mid s^{\prime}\right)\right)\right)\right] \\ &=\underset{s^{\prime} \sim p\left(s^{\prime} \mid s, a\right)}{\mathbb{E}}\left[r(s, a)+\gamma V_{s o f t}^{\pi}\left(s^{\prime}\right)\right] \end{aligned} \]

其中

\[ \begin{aligned} V_{s o f t}^{\pi}(s) &=\mathbb{E}_{a \sim \pi}\left[Q_{s o f t}^{\pi}(s, a)\right]+\alpha H(\pi(\cdot \mid s)) \\&=\mathbb{E}_{a \sim \pi}\left[Q_{s o f t}^{\pi}(s, a)\right]-\alpha \mathbb{E}_{a \sim \pi}\left[(\log \pi(a \mid s) \right]\\ &=\underset{a \sim \pi}{\mathbb{E}}\left[Q_{s o f t}^{\pi}(s, a)-\alpha \log \pi(a \mid s)\right] \end{aligned} \]

上面的最大熵Q、V的定义用在SAC中，而Soft Q Learning一开始用的是另一套式子

1.5 策略的形式

在1.3、1.4节我们知道了值函数的形式，问题在于，我们最终的目的还是要得到一个策略，那策略是什么形式呢？

还记得价值函数$V$的表示不？

\[ V\left(\mathbf{s}_{t}\right)=\mathbb{E}_{\mathbf{a}_{t} \sim \pi}\left[Q\left(\mathbf{s}_{t}, \mathbf{a}_{t}\right)-\alpha \log \pi\left(\mathbf{a}_{t} \mid \mathbf{s}_{t}\right)\right] \] 从$V$的表达式中可以反解出$\pi$的形式，移项后可得：

\[ \mathbb{E}_{\mathbf{a}_{t} \sim \pi}\left[Q\left(\mathbf{s}_{t}, \mathbf{a}_{t}\right)-\alpha\log \pi\left(\mathbf{a}_{t} \mid \mathbf{s}_{t}\right)-V\left(\mathbf{s}_{t}\right)\right]=0 \] 其中一个解为 \[ \begin{aligned} \pi\left(s_{t}|a_{t}\right) &=\exp \left(\frac{1}{\alpha}\left(Q_{s o f t}\left(s_{t}, a_{t}\right)-V_{s o f t}\left(s_{t}\right)\right)\right) \\ &=\frac{\exp \left(\frac{1}{\alpha} Q_{\text {soft }}\left(s_{t}, a_{t}\right)\right)}{\exp \left(\frac{1}{\alpha} V_{\text {soft }}\left(s_{t}\right)\right)} \end{aligned} \]

于是我们得到了策略的形式。

注意，策略的形式不一定是这个，但是这样的策略一定满足最大熵的值函数约束，这意味着我们可以直接采用这种形式的策略来进行策略迭代。

1.6 状态价值函数V的另一种形式

注意到1.5节推导出的策略形式： \[ \begin{aligned} \pi\left(s_{t}|a_{t}\right) =\frac{\exp \left(\frac{1}{\alpha} Q_{\text {soft }}\left(s_{t}, a_{t}\right)\right)}{\exp \left(\frac{1}{\alpha} V_{\text {soft }}\left(s_{t}\right)\right)} \end{aligned} \]

由于策略所有动作概率积分为1：

\[ \int\pi\left(s_{t}|a_{t}\right)d \mathbf{a} =\frac{\int\exp \left(\frac{1}{\alpha} Q_{\text {soft }}\left(s_{t}, a_{t}\right)\right)d a}{\exp \left(\frac{1}{\alpha} V_{\text {soft }}\left(s_{t}\right)\right)}=1 \]

可以直接得到$V$与$Q$的第二种关系：

\[ V_{\text {soft }}\left(s_{t}\right) \triangleq \alpha \log \int \exp \left(\frac{1}{\alpha} Q_{\text {soft }}\left(s_{t}, a\right)\right) d a \]

注意，这种V和Q的关系的前提在于，策略π取1.5节推导出的特殊形式。 这也是Soft Q Learning中采用的形式

将上式回代得$\pi\left(s_{t}|a_{t}\right)$的另一种形式： \[ \begin{aligned} \pi\left(s_{t}|a_{t}\right)=\frac{\exp \left(\frac{1}{\alpha} Q_{\text {soft }}\left(s_{t}, a_{t}\right)\right)}{\exp \left(\frac{1}{\alpha} V_{\text {soft }}\left(s_{t}\right)\right)} =\frac{\exp \left(\frac{1}{\alpha} Q_{\text {soft }}\left(s_{t}, a_{t}\right)\right)}{ \int \exp \left(\frac{1}{\alpha} Q_{\text {soft }}\left(s_{t}, a\right)\right) d \mathbf{a}} \end{aligned} \]

1.7 最优策略

注意到最大熵的策略就是最大化$V$的策略，因此直接对$V$求$\pi$的泛函导数，令其为0，得到的就是最优策略：

\[ Q\left(\mathbf{s}_{t}, \mathbf{a}_{t}\right)-\alpha\log \pi\left(\mathbf{a}_{t} \mid \mathbf{s}_{t}\right)-\alpha=0 \\ \begin{aligned} \pi\left(s_{t}|a_{t}\right) =\frac{\exp \left(\frac{1}{\alpha} Q_{\text {soft }}\left(s_{t}, a_{t}\right)\right)}{e} \end{aligned} \] 又因为

\[ \int\pi\left(s_{t}|a_{t}\right)d \mathbf{a} =\frac{\int\exp \left(\frac{1}{\alpha} Q_{\text {soft }}\left(s_{t}, a_{t}\right)\right)d a}{e}=1 \\ \int\exp \left(\frac{1}{\alpha} Q_{\text {soft }}\left(s_{t}, a_{t}\right)\right) da=e \]

将分母中的e用上式代替，所以

\[ \begin{aligned} \pi\left(s_{t}|a_{t}\right) =\frac{\exp \left(\frac{1}{\alpha} Q_{\text {soft }}\left(s_{t}, a_{t}\right)\right)}{ \int \exp \left(\frac{1}{\alpha} Q_{\text {soft }}\left(s_{t}, a\right)\right) d \mathbf{a}} \end{aligned} \]

而1.6节推出的符合条件的策略形式为：

\[ \begin{aligned} \pi\left(s_{t}|a_{t}\right)=\frac{\exp \left(\frac{1}{\alpha} Q_{\text {soft }}\left(s_{t}, a_{t}\right)\right)}{\exp \left(\frac{1}{\alpha} V_{\text {soft }}\left(s_{t}\right)\right)} =\frac{\exp \left(\frac{1}{\alpha} Q_{\text {soft }}\left(s_{t}, a_{t}\right)\right)}{ \int \exp \left(\frac{1}{\alpha} Q_{\text {soft }}\left(s_{t}, a\right)\right) d \mathbf{a}} \end{aligned} \] 符合最优策略的形式

因此，1.5节推出的策略是最优策略。

又因为在Soft Q Learing论文附录中的A.2，最优策略是唯一的。

因此，1.5节推出的策略是唯一的最优策略。

至此，我们已经完全分析推导了最大熵框架下的价值函数V、Q，策略π的形式。

2、能量模型

还记得最大熵模型中推导出的最优策略形式不？

这到底是个什么东西？

Soft Q Learning中说它是能量模型，为什么这个东西就是能量模型了？

在推导完公式之后，还得了解我们推导的到底是个什么东西，这就是这节需要讲的能量模型了。

2.1 为什么要使用能量模型？

说到能量模型，就不得不提深度学习三巨头之一的Yann LeCun了。其凭借着能量模型在生成模型领域大行其道，并提出了“能量模型是通向自主人工智能系统的起点”、“已经做好放弃概率论的准备”等言论。

所以为什么他这么推崇能量模型呢？

用他综述里的话来说，就是：

基于能量的学习为许多概率和非概率的学习方法提供了一个统一的框架，特别是图模型和其他结构化模型的非概率训练。基于能量的学习可以被看作是预测、分类或决策任务的概率估计的替代方法。由于不需要适当的归一化，基于能量的方法避免了概率模型中与估计归一化常数相关的问题。此外，由于没有标准化条件，在学习机器的设计中允许了更多的灵活性。大多数概率模型都可以看作是特殊类型的基于能量的模型，其中能量函数满足一定的归一化条件，损失函数通过学习优化，具有特定的形式。

2.2 能量模型的含义

对于基本的能量函数而言，给定一个 X ，模型产生与 X 最兼容的Y

\[ Y^*=\arg\min_{Y\in\mathcal{Y}} E(Y,X)\\ \]

其中“最兼容”是指：==小能量值==对应于变量的==高度兼容==，而==大能量值==对应于变量的==高度不兼容==。

即能量函数要满足下面的性质：

给定一个$X$，输出的最优$Y$值让能量函数最小

能量函数在不同的技术社区中有不同的名称；它们可以被称为对比函数、价值函数或负对数似然函数。
能量函数可以是任意的，只要满足最优的$Y$能让能量最小即可。
举个例子，监督学习中的图片为$X$，标签为$Y_0（X）$，能量模型$E（X，Y）=（Y-Y_0（X))^2$，输出的Y越接近X 的标签，能量越低。此时监督学习的loss就是能量函数

2.3 能量函数的建模

对于决策任务，例如操纵机器人，只需要系统给予正确答案就能获得最低的能量，其他答案获得的更大能量无关紧要（比如RL中我们只需要选择能量最低的action即可）。然而，一个系统的输出有时必须与另一个系统的输出相结合，或者提供给另一个系统作为输入(或者提供给人类决策者)。唯一一致的方法是将所有可能输出的能量转换成一个标准化的概率分布。最简单、最常用的方法即转化为Gibbs分布（又叫做玻尔兹曼分布）：

\[ P(Y \mid X)=\frac{e^{-\beta E(Y, X)}}{\int_{y \in \mathcal{Y}} e^{-\beta E(y, X)}} \]

玻尔兹曼分布是一种概率分布，它给出一个系统处于某种状态的机率，该几率是此状态下的能量及温度的函。给出为：
\[ p_{i} \propto e^{-\varepsilon_{i} /(k T)} \\ p_{i}=\frac{1}{Q} e^{-\varepsilon_{i} /(k T)}=\frac{e^{-\varepsilon_{i} /(k T)}}{\sum_{j=1}^{M} e^{-\varepsilon_{j} /(k T)}}* \]

其中 $\varepsilon$ 表示能量，k是玻尔兹曼常数，T是系统的绝对温度，M是系统可访问的所有状态的数量。

可以看到，能量越低，被选中的概率越高，即被选中的动作越优。

这满足能量函数的性质，所以玻尔兹曼分布是基于能量的分布

2.4 基于能量的强化学习

终于可以知道最大熵模型中的最优策略的含义是什么了：

\[ \begin{aligned} \pi\left(s_{t}|a_{t}\right) =\frac{\exp \left(\frac{1}{\alpha} Q_{\text {soft }}\left(s_{t}, a_{t}\right)\right)}{\exp \left(\frac{1}{\alpha} V_{\text {soft }}\left(s_{t}\right)\right)}=\frac{\exp \left(\frac{1}{\alpha} Q_{\text {soft }}\left(s_{t}, a_{t}\right)\right)}{ \int \exp \left(\frac{1}{\alpha} Q_{\text {soft }}\left(s_{t}, a\right)\right) d \mathbf{a}} \end{aligned} \] 如果取能量函数：

\[ \mathcal{E}\left(\mathbf{s}_{t}, \mathbf{a}_{t}\right)=-\frac{1}{\alpha} Q_{\operatorname{soft}}\left(\mathbf{s}_{t}, \mathbf{a}_{t}\right) \] 再让策略正比于负能量：

\[ \pi\left(\mathbf{a}_{t} \mid \mathbf{s}_{t}\right) \propto \exp \left(-\mathcal{E}\left(\mathbf{s}_{t}, \mathbf{a}_{t}\right)\right) \] 这不就是玻尔兹曼分布吗？其中不存在温度$kT$对系统概率的影响。

所以最大熵强化学习中的最优策略形式是玻尔兹曼分布，其中$ $是温度系数。 $\alpha$ 越大，各个动作被选中的概率差就越小，越接近随机策略； $\alpha$ 越小，各个动作被选中的概率差就越大，越接近确定性策略。通过调节 $\alpha$ 可以调节策略的随机性探索。

把强化学习的策略建模为玻尔兹曼分布的想法之前就有过很多，并被称为玻尔兹曼探索，这样子做有个好处就是用随机策略可以加强探索，并且满足$Q$越大被选中的概率越大的条件。

2.5 能量策略的好处

这时候就要祭出这张经典的图了：

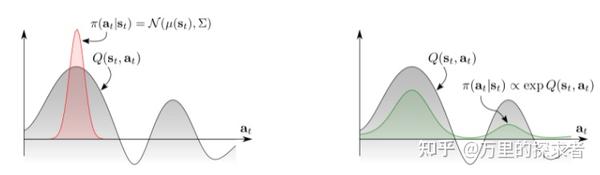
能量策略

传统的基于高斯分布的策略只能捕获单峰的Q值，也就是只能捕获一种行为模式，这种玻尔兹曼分布的能量策略能够捕获多个行为模式，大大增强了表达能力。

经过前面一大通的推导，现在我们已经理解了基于最大熵和能量模型的强化学习框架，也知道了其中值函数、策略的表达式。

接下来，根据这个框架，可以导出两个算法。

第一种，就是类似Q Learning风格的，Soft Q Learning。

3.1 Soft 值迭代

再次请出我们的Q和V函数：

\[ \begin{aligned} Q_{s o f t}(s, a) =\underset{s^{\prime} \sim p\left(s^{\prime} \mid s, a\right)}{\mathbb{E}}\left[r(s, a)+\gamma V_{s o f t}\left(s^{\prime}\right)\right] \end{aligned} \]

\[ V_{\text {soft }}\left(s_{t}\right) \triangleq \alpha \log \int \exp \left(\frac{1}{\alpha} Q_{\text {soft }}\left(s_{t}, a\right)\right) d \mathbf{a} \]

那么如何迭代更新得到他们呢？

只需要把“=”号改成迭代的形式即可：

\[ \begin{aligned} &Q_{\mathrm{soft}}\left(\mathbf{s}_{t}, \mathbf{a}_{t}\right) \leftarrow r_{t}+\gamma \mathbb{E}_{\mathbf{s}_{t+1} \sim p_{\mathbf{s}}}\left[V_{\mathrm{soft}}\left(\mathbf{s}_{t+1}\right)\right], \forall \mathbf{s}_{t}, \mathbf{a}_{t} \\&V_{\mathrm{soft}}\left(\mathbf{s}_{t}\right) \leftarrow \alpha \log \int_{\mathcal{A}} \exp \left(\frac{1}{\alpha} Q_{\mathrm{soft}}\left(\mathbf{s}_{t}, \mathbf{a}^{\prime}\right)\right) d \mathbf{a}^{\prime}, \forall \mathbf{s}_{t} \end{aligned} \]

收敛性证明见SQL附录，思路是利用压缩映射的证明方式。

只要不断地这么更新，值函数就会收敛。

3.2 参数化的Soft 值优化

在离散的情况下，只需要进行soft 价值迭代就行了。

为了进一步增强值函数的表示能力，可以将其用 $\theta$ 参数化（例如神经网络参数）变成 $Q_{\mathrm{soft}}^{\theta}\left(\mathbf{s}_{t}, \mathbf{a}_{t}\right)$和 $V_{}^{}(_{t}) $，使其适应连续的状态空间，并且可以使用梯度下降法来优化。

V：

求V的话需要对动作进行积分，这在动作空间特别大或者连续动作空间的时候是不可能的，因此可以考虑使用重要性采样对其分布进行估计：

\[ V_{\mathrm{soft}}^{\theta}\left(\mathbf{s}_{t}\right)=\alpha \log \mathbb{E}_{q_{\mathbf{a}^{\prime}}}\left[\frac{\exp \left(\frac{1}{\alpha} Q_{\mathrm{soft}}^{\theta}\left(\mathbf{s}_{t}, \mathbf{a}^{\prime}\right)\right)}{q_{\mathbf{a}^{\prime}}\left(\mathbf{a}^{\prime}\right)}\right] \]

$q_{^{}} $ 的话可以是任意分布，初期可以用随机分布，后面可以用当前策略。

Q：

求Q的话只需要类似DQN的更新就行了：

\[ J_{Q}(\theta)=\mathbb{E}_{\mathbf{s}_{t} \sim q_{\mathrm{s}_{t}}, \mathbf{a}_{t} \sim q_{\mathbf{a}_{t}}}\left[\frac{1}{2}\left(\hat{Q}_{\mathrm{soft}}^{\bar{\theta}}\left(\mathbf{s}_{t}, \mathbf{a}_{t}\right)-Q_{\mathrm{soft}}^{\theta}\left(\mathbf{s}_{t}, \mathbf{a}_{t}\right)\right)^{2}\right] \]

其中

\[ \hat{Q}_{\mathrm{soft}}^{\bar{\theta}}\left(\mathbf{s}_{t}, \mathbf{a}_{t}\right)=r_{t}+\gamma \mathbb{E}_{\mathbf{s}_{t+1} \sim p_{\mathrm{s}}}\left[V_{\mathrm{soft}}^{\bar{\theta}}\left(\mathbf{s}_{t+1}\right)\right] \]

对他们进行随机梯度下降就行了。

$q_{\mathrm{s}_{t}}$是当前策略。

但是还有一个问题，策略表示是玻尔兹曼分布： \[ \pi\left(\mathbf{a}_{t} \mid \mathbf{s}_{t}\right) \propto\exp \left(\frac{1}{\alpha} Q_{\mathrm{soft}}^{\theta}\left(\mathbf{s}_{t}, \mathbf{a}_{t}\right)\right) \]

如果是离散空间还好，连续空间怎么从这个玻尔兹曼分布进行抽样呢？

换言之，玻尔兹曼分布怎么用策略表示呢？

3.3 策略的近似采样

作者使用了一个可以用来表示策略的网络来代替玻尔兹曼分布的策略进行采样。随后利用KL散度来缩小用策略网络$\pi^\phi$与基于能量的策略之间的差距：

\[ \begin{aligned} J_{\pi}\left(\phi ; \mathbf{s}_{t}\right)= \mathrm{D}_{\mathrm{KL}}\left(\pi^{\phi}\left(\cdot \mid \mathbf{s}_{t}\right) \| \exp \left(\frac{1}{\alpha}\left(Q_{\mathrm{soft}}^{\theta}\left(\mathbf{s}_{t}, \cdot\right)-V_{\mathrm{soft}}^{\theta}\right)\right)\right) \end{aligned} \]

作者用了变分梯度下降进行优化。

不过这种采样网络在SAC的时候被弃掉了，估计可能是又复杂又用处不大

这个采样网络的存在可以看做是actor-critic中的actor。

3.4 Soft Q Learning

OK，现在价值函数和策略的采样更新方式都有了，就可以写算法了：

soft q learning

4、Soft Actor Critic

到了喜闻乐见的SAC环节。

4.1 Soft 策略迭代（Policy Iteration）

首先先介绍一下 Policy Iteration：它是一种在 Policy Evaluation 和 Policy Improvement 中交替迭代更新的强化学习方法。用大白话来讲的话，Policy Evaluation就是在估计某个状态执行某个动作平均能获得多少回报；而Policy Improvement 则是将策略调整为执行当前状态具有更大回报的动作。

SAC抛弃了对动作进行积分的V函数： $V_{\text {soft }}\left(s_{t}\right) \triangleq \alpha \log \int \exp \left(\frac{1}{\alpha} Q_{\text {soft }}\left(s_{t}, a\right)\right) d \mathbf{a}$

采用了另一种V函数： \[ V\left(\mathbf{s}_{t}\right)=\mathbb{E}_{\mathbf{a}_{t} \sim \pi}\left[Q\left(\mathbf{s}_{t}, \mathbf{a}_{t}\right)-\log \pi\left(\mathbf{a}_{t} \mid \mathbf{s}_{t}\right)\right] \]

这样做就消除了V对动作积分难的问题

利用强化学习中的策略迭代方法，每次策略改进得到更好的策略，然后为新策略评估一个价值函数，然后继续改进策略，以此类推。就可以得到一个最优策略。

1）策略估计（Policy Evaluation）

首先需要了解贝尔曼方程： \[ Q(s_t,a_t)=r(s_t,a_t)+\gamma\sum_{s^{\prime}\in S}P(s^{\prime}|s)V(s^{\prime})=r(s_t,a_t)+\gamma\mathbb{E}_{\mathbf{s}_{t+1}\sim p}\left[V(\mathbf{s}_{t+1})\right] \] 对其==考虑熵==，定义一个考虑熵的$Q(s,a)$为 $\mathcal{T}^π Q ( s_t , a_t )$。~~不断对价值函数运用贝尔曼算子，价值函数就能够收敛到策略$\pi$下的价值估计：~~ \[ \mathcal{T}^{\pi} Q\left(\mathbf{s}_{t}, \mathbf{a}_{t}\right) \triangleq r\left(\mathbf{s}_{t}, \mathbf{a}_{t}\right)+\gamma \mathbb{E}_{\mathbf{s}_{t+1} \sim p}\left[V\left(\mathbf{s}_{t+1}\right)\right]，其中V(\mathbf{s}_{t+1})=\mathbb{E}_{\mathbf{a}_{t+1}\sim\pi}\left[Q(\mathbf{s}_{t+1},\mathbf{a}_{t+1})-\log\pi(\mathbf{a}_{t+1}|\mathbf{s}_{t+1})\right] \]

\[ \mathcal{T}^{\pi} Q\left(\mathbf{s}_{t}, \mathbf{a}_{t}\right) \triangleq r\left(\mathbf{s}_{t}, \mathbf{a}_{t}\right)+\gamma \mathbb{E}_{\mathbf{s}_{t+1} \sim p,{\mathbf{a}_{t+1}}\sim\pi}\left[Q(\mathbf{s}_{t+1},\mathbf{a}_{t+1})-\log\pi(\mathbf{a}_{t+1}|\mathbf{s}_{t+1})\right] \]

证明：把奖励$r$和熵写到一起，因此最大熵目标变成了包含熵的奖励： \[ r_{\pi}\left(\mathbf{s}_{t}, \mathbf{a}_{t}\right) \triangleq r\left(\mathbf{s}_{t}, \mathbf{a}_{t}\right)+\mathbb{E}_{\mathbf{s}_{t+1} \sim p}\left[\mathcal{H}\left(\pi\left(\cdot \mid \mathbf{s}_{t+1}\right)\right)\right] \] 而这种修改了的奖励形式恰好符合策略估计的收敛证明：
\[ Q\left(\mathbf{s}_{t}, \mathbf{a}_{t}\right) \leftarrow r_{\pi}\left(\mathbf{s}_{t}, \mathbf{a}_{t}\right)+\gamma \mathbb{E}_{\mathbf{s}_{t+1} \sim p, \mathbf{a}_{t+1} \sim \pi}\left[Q\left(\mathbf{s}_{t+1}, \mathbf{a}_{t+1}\right)\right] \] 所以价值函数收敛

2）策略改进（Policy Improvement）

在1、2节我们知道，最优策略是采用玻尔兹曼分布能量形式的策略

SAC利用这一点来更新策略：

\[ \pi_{\text {new }}=\arg \min _{\pi^{\prime} \in \Pi} \mathrm{D}_{\mathrm{KL}}\left(\pi^{\prime}\left(\cdot \mid \mathbf{s}_{t}\right) \| \frac{\exp \left(Q^{\pi_{\mathrm{old}}}\left(\mathbf{s}_{t}, \cdot\right)\right)}{Z^{\pi_{\text {old }}}\left(\mathbf{s}_{t}\right)}\right) \]

但是并没有直接采用玻尔兹曼分布，而是通过高斯分布来近似玻尔兹曼分布，因为高斯分布更好处理一些。

但是这样直接丢失了玻尔兹曼分布捕获多峰函数的能力

$Z$是归一化函数。在上式中，我们先将$Q^{\pi_{old}}_{soft}$指数化为$\exp(\alpha^{-1}{Q^{\pi_{old}}_{soft}})$再将其归一化为分布$\frac{\exp \left(Q^{\pi_{\mathrm{old}}}\left(\mathbf{s}_{t}, \cdot\right)\right)}{Z^{\pi_{\text {old }}}\left(\mathbf{s}_{t}\right)}$，其中$Z^{\pi_{old}}(s_t)=\int \exp(\alpha^{-1}{Q^{\pi_{old}}_{soft}}) da_t$为归一化函数。我们希望找到一个策略$\pi \prime$在状态$s_t$下的动作分布与$\frac{\exp \left(Q^{\pi_{\mathrm{old}}}\left(\mathbf{s}_{t}, \cdot\right)\right)}{Z^{\pi_{\text {old }}}\left(\mathbf{s}_{t}\right)}$分布的KL-divergence最小，即希望$\pi \prime(\cdot|s_t)$与分布$\frac{\exp \left(Q^{\pi_{\mathrm{old}}}\left(\mathbf{s}_{t}, \cdot\right)\right)}{Z^{\pi_{\text {old }}}\left(\mathbf{s}_{t}\right)}$越相似越好。采用普通的策略优化只会在最高峰满足相似性，而soft策略优化会在整个分布上尽量与价值函数保持相似，不仅保证了赋予动作价值更高的动作更大的概率，还保证了新策略具有较大的熵。过程如下图所示：

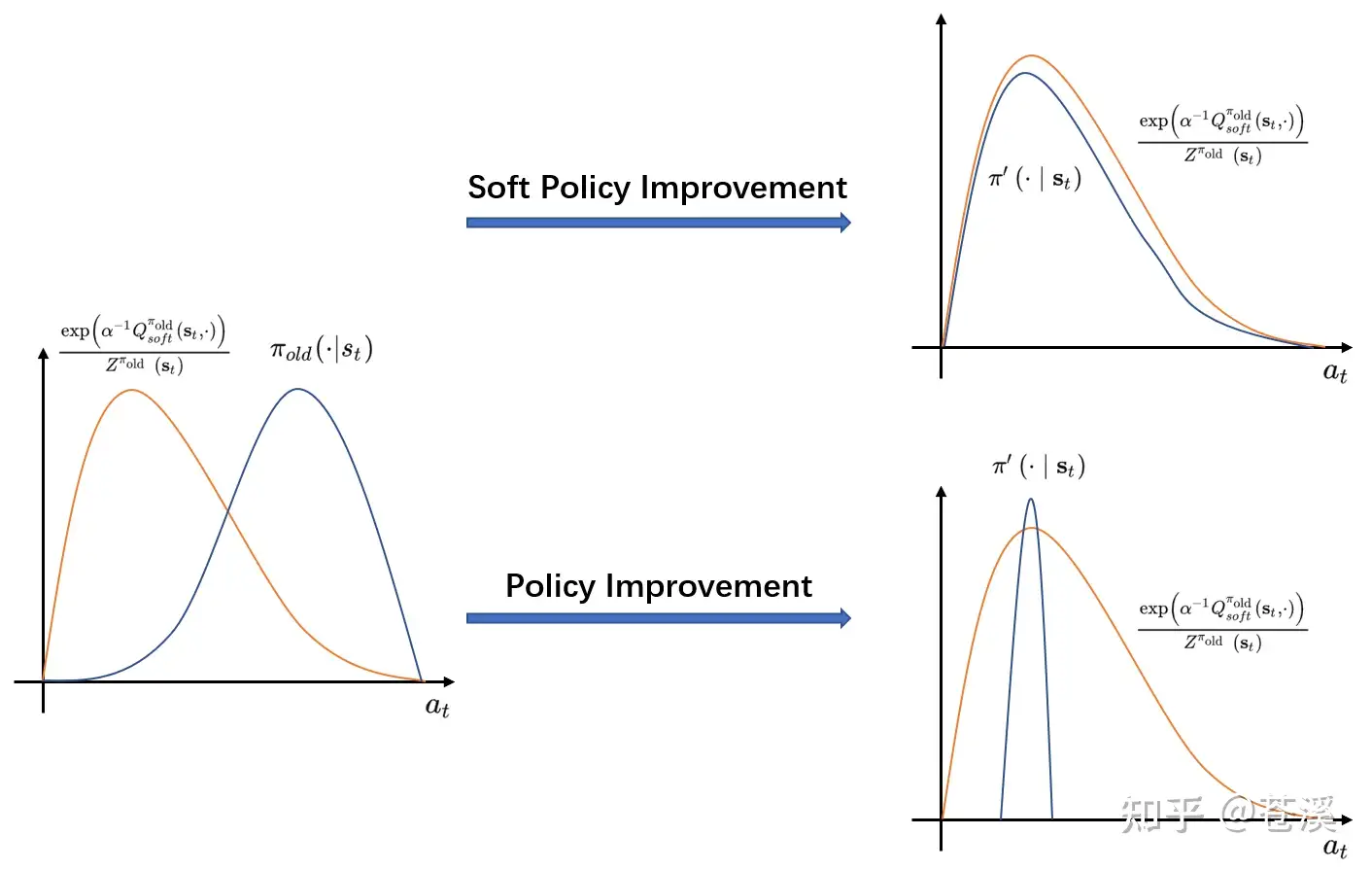
4.2 参数化的SAC算法

类似Soft Q Learning，SAC也将价值函数 $V_{}(_{t}) $、 $Q_{\theta}\left(\mathbf{s}_{t}, \mathbf{a}_{t}\right)$ 和策略 $\pi_{\phi}\left(\mathbf{a}_{t} \mid \mathbf{s}_{t}\right)$ 参数化来表达连续域与方便优化。

1）价值函数的优化

价值函数的优化都类似DQN算法，通过极小化Soft Bellman residual实现，下式中$D$为回放缓冲区（Replay Buffer）：

优化$V$的目标函数：

\[ J_{V}(\psi)=\mathbb{E}_{\mathbf{s}_{t} \sim \mathcal{D}}\left[\frac{1}{2}\left(V_{\psi}\left(\mathbf{s}_{t}\right)-\mathbb{E}_{\mathbf{a}_{t} \sim \pi_{\phi}}\left[Q_{\theta}\left(\mathbf{s}_{t}, \mathbf{a}_{t}\right)-\log \pi_{\phi}\left(\mathbf{a}_{t} \mid \mathbf{s}_{t}\right)\right]\right)^{2}\right] \]

随机梯度：

\[ \hat{\nabla}_{\psi} J_{V}(\psi)=\nabla_{\psi} V_{\psi}\left(\mathbf{s}_{t}\right)\left(V_{\psi}\left(\mathbf{s}_{t}\right)-Q_{\theta}\left(\mathbf{s}_{t}, \mathbf{a}_{t}\right)+\log \pi_{\phi}\left(\mathbf{a}_{t} \mid \mathbf{s}_{t}\right)\right) \]

优化$Q$的目标函数：

\[ J_{Q}(\theta)=\mathbb{E}_{\left(\mathbf{s}_{t}, \mathbf{a}_{t}\right) \sim \mathcal{D}}\left[\frac{1}{2}\left(Q_{\theta}\left(\mathbf{s}_{t}, \mathbf{a}_{t}\right)-\hat{Q}\left(\mathbf{s}_{t}, \mathbf{a}_{t}\right)\right)^{2}\right] \]

其中：

\[ \hat{Q}\left(\mathbf{s}_{t}, \mathbf{a}_{t}\right)=r\left(\mathbf{s}_{t}, \mathbf{a}_{t}\right)+\gamma \mathbb{E}_{\mathbf{s}_{t+1} \sim p}\left[V_{\bar{\psi}}\left(\mathbf{s}_{t+1}\right)\right] \]

随机梯度：

\[ \hat{\nabla}_{\theta} J_{Q}(\theta)=\nabla_{\theta} Q_{\theta}\left(\mathbf{a}_{t}, \mathbf{s}_{t}\right)\left(Q_{\theta}\left(\mathbf{s}_{t}, \mathbf{a}_{t}\right)-r\left(\mathbf{s}_{t}, \mathbf{a}_{t}\right)-\gamma V_{\bar{\psi}}\left(\mathbf{s}_{t+1}\right)\right) \]

同样用到了target网络$V_{\bar{\psi}}$

2）策略的优化

同样用一个高斯分布通过KL散度近似玻尔兹曼分布： \[ J_{\pi}(\phi)=\mathbb{E}_{\mathbf{s}_{t} \sim \mathcal{D}}\left[\mathrm{D}_{\mathrm{KL}}\left(\pi_{\phi}\left(\cdot \mid \mathbf{s}_{t}\right) \| \frac{\exp \left(Q_{\theta}\left(\mathbf{s}_{t}, \cdot\right)\right)}{Z_{\theta}\left(\mathbf{s}_{t}\right)}\right)\right] \]

对此有两种好用的优化方法

策略梯度方法：SAC的策略梯度参考这篇，是可以推导出来的。
重参数化技巧，也是SAC实际运用的方法：

\[ \begin{aligned} D_{KL}(p||q)&=H(p,q)-H(p) \\ &=- \sum_x p(x)\log q(x)- (-\sum_xp(x)\log p(x)) \\ &=- \sum_x p(x)(\log q(x)-\log p(x)) \\ &=- \sum_x p(x)\log \frac{q(x)}{p(x)} \end{aligned} \]

把策略的目标函数化简： $$ \[\begin{aligned} &\underset{\phi}{\operatorname{minimize}} D_{K L}\left(\pi_\phi\left(\cdot \mid s_t\right) \| \frac{\exp(\alpha ^{-1}Q_\theta\left(s_t, a_t\right))}{\exp(\log \left(Z_\theta\left(s_t\right)\right))}\right) \\&=\underset{\phi}{\operatorname{minimize}} D_{K L}\left(\pi_\phi\left(\cdot \mid s_t\right) \| \exp \left[\alpha ^{-1}Q_\theta\left(s_t, a_t\right)-\log \left(Z_\theta\left(s_t\right)\right)\right]\right) \\ &=\underset{\phi}{\operatorname{minimize}} \sum_{a_t}\left[\log \pi_\phi\left(a_t \mid s_t\right)-\alpha ^{-1}Q_\theta\left(s_t, a_t\right)+\log \left(Z_\theta\left(s_t\right)\right]\right. \\ &=\underset{\phi}{\operatorname{minimize}} \underset{a_t \sim \pi_\phi\left(\cdot| s_t\right)}{\mathbb{E}}\left[\log \pi_\phi\left(a_t \mid s_t\right)-\alpha ^{-1}Q_\theta\left(s_t, a_t\right)+\log \left(Z_\theta\left(s_t\right)\right]\right. \\ &=\underset{\phi}{\operatorname{minimize}} \underset{a_t \sim \pi_\phi\left(\cdot| s_t\right)}{\mathbb{E}}\left[\alpha \log \pi_\phi\left(a_t \mid s_t\right)-Q_\theta\left(s_t, a_t\right)\right] \\ \end{aligned}\]

\[ J_{\pi}(\phi)=E_{s_{t} \sim D, a_{t} \sim \pi_{\phi}}\left[\log _{\pi_{\phi}}\left(a_{t} \mid s_{t}\right)-\frac{1}{\alpha} Q_{\theta}\left(s_{t}, a_{t}\right)\right] \]

如果直接对其求策略梯度的话，是不能把直接对期望里面的项求梯度的，因为期望包含了策略，因此必须对期望进行解耦，使其与策略无关。

直接把动作建模为取决于噪声分布和状态分布的网络：

\[ \mathbf{a}_{t}=f_{\phi}\left(\epsilon_{t} ; \mathbf{s}_{t}\right) \]

其中$ _{t} $是取自诸如高斯分布的噪声。

因此目标函数就变为：

\[ J_{\pi}(\phi)=\mathbb{E}_{\mathbf{s}_{t} \sim \mathcal{D}, \epsilon_{t} \sim \mathcal{N}}\left[\log \pi_{\phi}\left(f_{\phi}\left(\epsilon_{t} ; \mathbf{s}_{t}\right) \mid \mathbf{s}_{t}\right)-Q_{\theta}\left(\mathbf{s}_{t}, f_{\phi}\left(\epsilon_{t} ; \mathbf{s}_{t}\right)\right)\right] \]

可以看到期望里的噪声分布和策略参数解耦了

因此就可以直接对其求梯度了，不用管期望里的分布了：

\[ \begin{aligned} \hat{\nabla}_{\phi} J_{\pi}(\phi)=\nabla_{\phi} \log \pi_{\phi}\left(\mathbf{a}_{t} \mid \mathbf{s}_{t}\right)d+\left(\nabla_{\mathbf{a}_{t}} \log \pi_{\phi}\left(\mathbf{a}_{t} \mid \mathbf{s}_{t}\right)-\nabla_{\mathbf{a}_{t}} Q\left(\mathbf{s}_{t}, \mathbf{a}_{t}\right)\right) \nabla_{\phi} f_{\phi}\left(\epsilon_{t} ; \mathbf{s}_{t}\right) \end{aligned} \]

注意，不用重参数化技巧也可以。如果直接对期望求梯度也是可以做的，那样就利用了策略梯度方法的思想。
重参数化技巧的额外好处是方差小，SAC用重参数化技巧其实是这个原因。

4.3 SAC算法

SAC又从别的算法里抄了几个trick，比如TD3的双Q网络取最小、还有DQN的trick，不过这些都不重要。

经过上面的分析，价值函数和策略的更新都了解了，可以写出算法了：

SAC算法

5、SAC2：自动调整温度系数

SAC算法对于温度参数非常敏感，而调整热度参数是又比较困难——我们怎么确定在每一时刻用什么温度参数呢？只需要保证每一步的熵都不低于一个最小值就行了，即求解如下约束优化问题：

\[ \max _{\pi_{0}, \ldots, \pi_{T}} \mathbb{E}\left[\sum_{t=0}^{T} r\left(s_{t}, a_{t}\right)\right] \text { s.t. } \forall t, \mathcal{H}\left(\pi_{t}\right) \geq \mathcal{H}_{0} \]

因为在时刻t的策略不会影响到之前时刻的策略，我们可以用类似动态规划的思想从后往前逐步最大化收益：

\[ \max _{\pi 0}\left(\mathbb{E}\left[r\left(s_{0}, a_{0}\right)\right]+\max _{\pi_{1}}\left(\mathbb{E}[\ldots]+\max _{\pi_{T}} \mathbb{E}\left[r\left(s_{T}, a_{T}\right)\right]\right)\right) \]

我们从最后一个时刻T开始最大化：

\[ \mathbb{E}_{\left(s_{T}, a_{T}\right) \sim \rho_{\pi}}\left[r\left(s_{T}, a_{T}\right)\right] \text { s.t. } \mathcal{H}\left(\pi_{T}\right)-\mathcal{H}_{0} \geq 0 \]

要求解这个问题，需要用到拉格朗日对偶的方法。

拉格朗日对偶这个写的非常好：笨蛋都能看懂的拉格朗日对偶
知道了拉格朗日对偶的做法，就可以继续下面的推导啦

首先，我们定义以下函数：

\[ \begin{aligned} h\left(\pi_{T}\right) &=\mathcal{H}\left(\pi_{T}\right)-\mathcal{H}_{0}=\mathbb{E}_{\left(s_{T}, a_{T}\right) \sim \rho_{\pi}}\left[-\log \pi_{T}\left(a_{T} \mid s_{T}\right)\right]-\mathcal{H}_{0} \\ f\left(\pi_{T}\right) &= \begin{cases}\mathbb{E}_{\left(s_{T}, a_{T}\right) \sim \rho_{\pi}}\left[r\left(s_{T}, a_{T}\right)\right], & \text { if } h\left(\pi_{T}\right) \geq 0 \\ -\infty, & \text { otherwise }\end{cases} \end{aligned} \]

于是优化问题就变成了：

\[ f\left(\pi_{T}\right) \text { s.t. } h\left(\pi_{T}\right) \geq 0 \]

为了解决这个不等式约束的最大化优化问题，我们可以构建一个带有拉格朗日乘子的表达式：

\[ L\left(\pi_{T}, \alpha_{T}\right)=f\left(\pi_{T}\right)+\alpha_{T} h\left(\pi_{T}\right) \]

实际上，目标函数就等价于最小化L的$\alpha$的式子：

\[ f\left(\pi_{T}\right)=\min _{\alpha_{T} \geq 0} L\left(\pi_{T}, \alpha_{T}\right) \]

这样写的原因如下：

如果约束被满足，那么 $\alpha$ 最好将其设置为0才能让L最小（注意 $ $ ）。于是。
如果约束被违背了，即，我们可以通过令$\alpha_{T} \rightarrow \infty$来使得$ L({T}, {T}) -$。于是$L({T}, )=-=f({T})$。

上面这个min仅仅代表的是约束条件的满足

为了最大化目标函数还需要一个max的操作： \[ \max _{\pi_{T}} f\left(\pi_{T}\right)=\max _{\pi_{T}}\min _{\alpha_{T} \geq 0} L\left(\pi_{T}, \alpha_{T}\right) \] 现在把它变成更好处理的对偶问题：

\[ \begin{aligned} \max _{\pi_{T}} \mathbb{E}\left[r\left(s_{T}, a_{T}\right)\right] &=\max _{\pi_{T}} f\left(\pi_{T}\right) \\ &=\min _{\alpha_{T} \geq 0} \max _{\pi_{T}} L\left(\pi_{T}, \alpha_{T}\right) \\ &=\min _{\alpha_{T} \geq 0} \max _{\pi_{T}} f\left(\pi_{T}\right)+\alpha_{T} h\left(\pi_{T}\right) \\ &=\min _{\alpha_{T} \geq 0} \max _{\pi_{T}} \mathbb{E}_{\left(s_{T}, a_{T}\right) \sim \rho_{\pi}}\left[r\left(s_{T}, a_{T}\right)\right]+\alpha_{T}\left(\mathbb{E}_{\left(s_{T}, a_{T}\right) \sim \rho_{\pi}}\left[-\log \pi_{T}\left(a_{T} \mid s_{T}\right)\right]-\mathcal{H}_{0}\right) \\ &=\min _{\alpha_{T} \geq 0} \max _{\pi_{T}} \mathbb{E}_{\left(s_{T}, a_{T}\right) \sim \rho_{\pi}}\left[r\left(s_{T}, a_{T}\right)-\alpha_{T} \log \pi_{T}\left(a_{T} \mid s_{T}\right)\right]-\alpha_{T} \mathcal{H}_{0} \\ &=\min _{\alpha_{T} \geq 0} \max _{\pi_{T}} \mathbb{E}_{\left(s_{T}, a_{T}\right) \sim \rho_{\pi}}\left[r\left(s_{T}, a_{T}\right)+\alpha_{T} \mathcal{H}\left(\pi_{T}\right)-\alpha_{T} \mathcal{H}_{0}\right] \end{aligned} \]

由于目标函数是线性的，熵约束是凸函数，所以强对偶性成立。
这意味着对偶问题的最优解等于原始问题的最优解。

所以最优策略和最优温度系数都可以表示出来了：

\[ \begin{aligned} &\pi_{T}^{\star}=\arg \max _{\pi_{T}} \mathbb{E}_{\left(s_{T}, a_{T}\right) \sim \rho_{\pi}}\left[\left(s_{T}, a_{T}\right)+\alpha_{T} \mathcal{H}\left(\pi_{T}\right)-\alpha_{T} \mathcal{H}_{0}\right] \\ &\alpha_{T}^{\star}=\arg \min _{\alpha_{T} \geq 0} \mathbb{E}_{\left(s_{T}, a_{T}\right) \sim \rho_{\pi^{\star}}}\left[\alpha_{T} \mathcal{H}\left(\pi_{T}^{\star}\right)-\alpha_{T} \mathcal{H}_{0}\right] \end{aligned} \]

所以目标函数的最大化完全可以用最优策略和温度系数表示：

\[ \max _{\pi_{T}} \mathbb{E}\left[r\left(s_{T}, a_{T}\right)\right]=\mathbb{E}_{\left(s_{T}, a_{T}\right) \sim \rho_{\pi^{\star}}}\left[r\left(s_{T}, a_{T}\right)+\alpha_{T}^{\star} \mathcal{H}\left(\pi_{T}^{\star}\right)-\alpha_{T}^{\star} \mathcal{H}_{0}\right] \]

把这个思想用到Q函数中，那么Q函数也可以这么表示：

\[ \begin{aligned} Q_{T-1}\left(s_{T-1}, a_{T-1}\right) &=r\left(s_{T-1}, a_{T-1}\right)+\mathbb{E}\left[Q\left(s_{T}, a_{T}\right)-\alpha_{T} \log \pi\left(a_{T} \mid s_{T}\right)\right] \\ &=r\left(s_{T-1}, a_{T-1}\right)+\mathbb{E}\left[r\left(s_{T}, a_{T}\right)\right]+\alpha_{T} \mathcal{H}\left(\pi_{T}\right) \\ Q_{T-1}^{\star}\left(s_{T-1}, a_{T-1}\right) &=r\left(s_{T-1}, a_{T-1}\right)+\max _{\pi_{T}} \mathbb{E}\left[r\left(s_{T}, a_{T}\right)\right]+\alpha_{T}^{\star} \mathcal{H}\left(\pi_{T}^{\star}\right) \end{aligned} \] 因此,回溯到T-1步，把最优Q的式子带进去，形成了另一个约束优化问题

同样使用拉格朗日对偶：

\[ \begin{aligned} &\max _{\pi_{T-1}}\left(\mathbb{E}\left[r\left(s_{T-1}, a_{T-1}\right)\right]+\max _{\pi_{T}} \mathbb{E}\left[r\left(s_{T}, a_{T}\right]\right)\right. \\ &=\max _{\pi_{T-1}}\left(Q_{T-1}^{\star}\left(s_{T-1}, a_{T-1}\right)-\alpha_{T}^{\star} \mathcal{H}\left(\pi_{T}^{\star}\right)\right) \\ &=\min _{\alpha_{T-1} \geq 0} \max _{\pi_{T-1}}\left(Q_{T-1}^{\star}\left(s_{T-1}, a_{T-1}\right)-\alpha_{T}^{\star} \mathcal{H}\left(\pi_{T}^{\star}\right)+\alpha_{T-1}\left(\mathcal{H}\left(\pi_{T-1}\right)-\mathcal{H}_{0}\right)\right) \\ &=\min _{\alpha_{T-1} \geq 0} \max _{\pi_{T-1}}\left(Q_{T-1}^{\star}\left(s_{T-1}, a_{T-1}\right)+\alpha_{T-1} \mathcal{H}\left(\pi_{T-1}\right)-\alpha_{T-1} \mathcal{H}_{0}\right)-\alpha_{T}^{\star} \mathcal{H}\left(\pi_{T}^{\star}\right) \end{aligned} \] 类似的，也可以得到T-1步的最优策略和最优温度系数：

\[ \begin{aligned} \pi_{T-1}^{\star} &=\arg \max _{\pi_{T-1}} \mathbb{E}_{\left(s_{T-1} a_{T-1}\right) \sim \rho_{\pi}}\left[Q_{T-1}^{\star}\left(s_{T-1}, a_{T-1}\right)+\alpha_{T-1} \mathcal{H}\left(\pi_{T-1}\right)-\alpha_{T-1} \mathcal{H}_{0}\right] \\ \alpha_{T-1}^{\star} &=\arg \min _{\alpha_{T-\mathbb{Z}}} \mathbb{E}_{\left(s_{T-1} a_{T-1}\right) \sim \rho_{\pi^{\star}}}\left[\alpha_{T-1} \mathcal{H}\left(\pi_{T-1}^{\star}\right)-\alpha_{T-1} \mathcal{H}_{0}\right] \end{aligned} \]

于是，在每一步我们都能够最小化以下目标函数以求解温度系数：

\[ J(\alpha)=\mathbb{E}_{a_{t} \sim \pi_{t}}\left[-\alpha \log \pi_{t}\left(a_{t} \mid \pi_{t}\right)-\alpha \mathcal{H}_{0}\right] \]

并得到最优温度系数：

\[ \alpha_{t}^{*}=\arg \min _{\alpha_{t}} \mathbb{E}_{\mathbf{a}_{t} \sim \pi_{t}^{*}}\left[-\alpha_{t} \log \pi_{t}^{*}\left(\mathbf{a}_{t} \mid \mathbf{s}_{t} ; \alpha_{t}\right)-\alpha_{t} \overline{\mathcal{H}}\right] \]

综上，把熵的自动求解放入SAC中，就形成了SAC2算法：

SAC2

6、SAC-离散

SAC当然是一个很好的想法，在很多连续动作空间的任务上都达到了SOTA，不过并不是很适合离散动作空间。

为了适应离散动作空间，必须要做出以下五个改变：

Q函数输出所有的状态动作。这在连续状态空间是不可能的，因为动作是连续的。在离散动作空间中这种情况就成为了提高效率的一种可能方法。
策略函数不输出均值和方差，直接输出动作分布。这是离散动作空间的必然要求。
对求V动作的期望改成积分。之前求V的时候需要对动作求期望：$V(s_{t}):=E_{a_{t} }$，不过在离散动作空间，所有动作的积分是可以求得的，因此变期望为积分以减少方差：$V(s_{t}):=(s_{t})^{T}$
同样的，对温度系数的动作期望改成积分。$J(\alpha)=\pi_{t}\left(s_{t}\right)^{T}\left[-\alpha\left(\log \left(\pi_{t}\left(s_{t}\right)\right)+\bar{H}\right)\right]$
去掉重参数化。之前使用重参数化的一个原因是期望里带动作分布，因此梯度不能从期望外直接提到期望内。但是现在动作已经变成积分/求和形式了，每个动作都能直接计算出来，因此可以直接对以下目标函数求梯度：$J_{\pi}(\phi)=E_{s_{t} \sim D}\left[\pi_{t}\left(s_{t}\right)^{T}\left[\alpha \log \left(\pi_{\phi}\left(s_{t}\right)\right)-Q_{\theta}\left(s_{t}\right)\right]\right]$

这五点构成了离散SAC算法：