归一化、标准化、正则化
本文最后更新于 2024年9月4日 下午
归一化(Normalization)
①把数据变为(0,1)或(-1,1)之间的小数。主要是为了方便数据处理,因为将数据映射到0~1范围之内,可以使处理过程更加便捷、快速。
②把有量纲表达式变换为无量纲表达式,成为纯量。经过归一化处理的数据,处于同一数量级,可以消除指标之间的量纲和量纲单位的影响,提高不同数据指标之间的可比性。
主要算法:
①线性转换,即min-max归一化(常用方法)
\[
y=\frac{x-min}{max-min}
\]
②对数函数转换 \[ y=\lg x \]
标准化(Standardization)
数据的标准化是将数据按比例缩放,使之落入一个小的特定区间。
主要算法:
①z-score标准化,即零-均值标准化(常用方法),其中\(\mu\)是样本数据的均值(mean),\(\sigma\)是样本数据的标准差(std) \[ y=\frac{x-\mu}{\sigma} \]
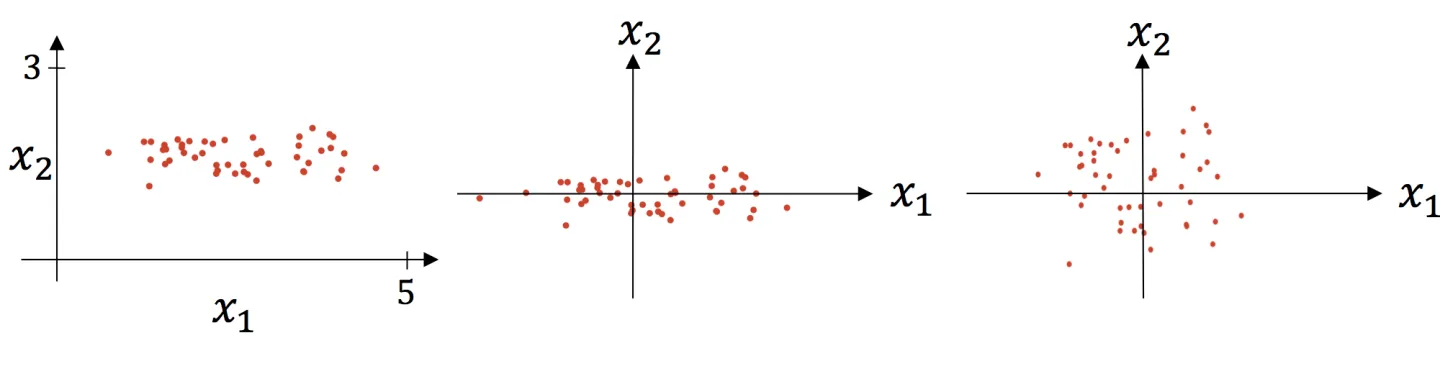
上图则是一个散点序列的标准化过程:原图->减去均值->除以标准差。
这是一种统计的处理,基于正态分布的假设,将数据变换为均值为0、标准差为1的标准正态分布。但即使数据不服从正态分布,也可以用此法。特别适用于数据的最大值和最小值未知,或存在孤立点。
②小数定标标准化
小数定标标准化通过移动x的小数位置进行标准化,将数据映射到[-1,1]区间上,移动的小数位数取决于数据绝对值的最大值。例如一组数据为[99,10,210,-90,-999],其中绝对值最大数为-999,那么所有数据小数点移动三位即可得到标准化后的数据[0.099,0.01,0.21,-0.09,-0.999]。 \[ y=\frac{x}{10^j},j 确保max(|y|)<1 \]
③ 对数Logistic模式 \[ y=\frac{1}{1+e^{-x}} \]
正则化(Regularization)
用一组与原不适定问题相“邻近”的适定问题的解,去逼近原问题的解,这种方法称为正则化方法。如何建立有效的正则化方法是反问题领域中不适定问题研究的重要内容。通常的正则化方法有基于变分原理的Tikhonov 正则化、各种迭代方法以及其它的一些改进方法。
总的来说,归一化是为了消除不同数据之间的量纲,方便数据比较和共同处理,比如在神经网络中,归一化可以加快训练网络的收敛性;标准化是为了方便数据的下一步处理,而进行的数据缩放等变换,并不是为了方便与其他数据一同处理或比较,比如数据经过零-均值标准化后,更利于使用标准正态分布的性质,进行处理;正则化而是利用先验知识,在处理过程中引入正则化因子(regulator),增加引导约束的作用,比如在逻辑回归中使用正则化,可有效降低过拟合的现象。
参考
归一化 (Normalization)、标准化 (Standardization)和中心化/零均值化 (Zero-centered) - 简书 (jianshu.com)